GIS with Python and IPython¶

Getting some data¶

There are many sources of GIS data. Here are some useful links:

  • WorldMap
  • FAO's GeoNetwork
  • IPUMS USA Boundary files for Censuses
  • IPUMS International Boundary files for Censuses
  • GADM database of Global Administrative Areas
  • Global Administrative Unit Layers
  • Natural Earth: All kinds of geographical, cultural and socioeconomic variables
  • Global Map
  • Digital Chart of the World
  • Sage and Sage Atlas
  • Caloric Suitability Index CSI: Agricultural suitability data
  • Ramankutti's Datasets on land use, crops, etc.
  • SEDAC at Columbia Univesrity: Gridded Population, Hazzards, etc.
  • World Port Index
  • USGS elevation maps
  • NOOA's Global Land One-km Base Elevation Project (GLOBE)
  • NOOA Nightlight data: This is the data used by Henderson, Storeygard, and Weil AER 2012 paper.
  • Other NOOA Data
  • GEcon
  • OpenStreetMap
  • U.S. Census TIGER
  • Geo-referencing of Ethnic Groups

See also Wikipedia links

Set-up¶

Let's import the packages we will use and set the paths for outputs.

In [1]:
# Let's import pandas and some other basic packages we will use 
from __future__ import division
%pylab --no-import-all
%matplotlib inline
import pandas as pd
import numpy as np
import os, sys

Using matplotlib backend: <object object at 0x1164f0770>
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
In [2]:
# GIS packages
import geopandas as gpd
from geopandas.tools import overlay
from shapely.geometry import Polygon, Point
import georasters as gr
# Alias for Geopandas
gp = gpd
In [3]:
# Plotting
import matplotlib as mpl
import seaborn as sns
# Setup seaborn
sns.set()
In [4]:
# Paths
pathout = './data/'

if not os.path.exists(pathout):
    os.mkdir(pathout)
    
pathgraphs = './graphs/'
if not os.path.exists(pathgraphs):
    os.mkdir(pathgraphs)

Initial Example -- Natural Earth Country Shapefile¶

Let's download a shapefile with all the polygons for countries so we can visualize and analyze some of the data we have downloaded in other notebooks. Natural Earth provides lots of free data so let's use that one.

For shapefiles and other polygon type data geopandas is the most useful package. geopandas is to GIS what pandas is to other data. Since gepandas extends the functionality of pandas to a GIS dataset, all the nice functions and properties of pandas are also available in geopandas. Of course, geopandas includes functions and properties unique to GIS data.

Next we will use it to download the shapefile (which is contained in a zip archive). geopandas extends pandas for use with GIS data. We can use many functions and properties of the GeoDataFrame to analyze our data.

In [5]:
import requests
import io

#headers = {'User-Agent': 'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_10_1) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/39.0.2171.95 Safari/537.36'}
headers = {'User-Agent': 'Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/51.0.2704.103 Safari/537.36', 'Accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8'}

url = 'https://naturalearth.s3.amazonaws.com/10m_cultural/ne_10m_admin_0_countries.zip'
r = requests.get(url, headers=headers)
countries = gp.read_file(io.BytesIO(r.content))
#countries = gpd.read_file('https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/10m/cultural/ne_10m_admin_0_countries.zip')

Let's look inside this GeoDataFrame

In [6]:
countries.head(10)
Out[6]:
featurecla scalerank LABELRANK SOVEREIGNT SOV_A3 ADM0_DIF LEVEL TYPE TLC ADMIN ... FCLASS_TR FCLASS_ID FCLASS_PL FCLASS_GR FCLASS_IT FCLASS_NL FCLASS_SE FCLASS_BD FCLASS_UA geometry
0 Admin-0 country 0 2 Indonesia IDN 0 2 Sovereign country 1 Indonesia ... None None None None None None None None None MULTIPOLYGON (((117.70361 4.16341, 117.70361 4...
1 Admin-0 country 0 3 Malaysia MYS 0 2 Sovereign country 1 Malaysia ... None None None None None None None None None MULTIPOLYGON (((117.70361 4.16341, 117.69711 4...
2 Admin-0 country 0 2 Chile CHL 0 2 Sovereign country 1 Chile ... None None None None None None None None None MULTIPOLYGON (((-69.51009 -17.50659, -69.50611...
3 Admin-0 country 0 3 Bolivia BOL 0 2 Sovereign country 1 Bolivia ... None None None None None None None None None POLYGON ((-69.51009 -17.50659, -69.51009 -17.5...
4 Admin-0 country 0 2 Peru PER 0 2 Sovereign country 1 Peru ... None None None None None None None None None MULTIPOLYGON (((-69.51009 -17.50659, -69.63832...
5 Admin-0 country 0 2 Argentina ARG 0 2 Sovereign country 1 Argentina ... None None None None None None None None None MULTIPOLYGON (((-67.19390 -22.82222, -67.14269...
6 Admin-0 country 3 3 United Kingdom GB1 1 2 Dependency 1 Dhekelia Sovereign Base Area ... Admin-0 dependency None Admin-0 dependency Admin-0 dependency Admin-0 dependency Admin-0 dependency Admin-0 dependency None Admin-0 dependency POLYGON ((33.78094 34.97635, 33.76043 34.97968...
7 Admin-0 country 1 5 Cyprus CYP 0 2 Sovereign country 1 Cyprus ... None None None None None None None None None MULTIPOLYGON (((33.78183 34.97622, 33.78094 34...
8 Admin-0 country 0 2 India IND 0 2 Sovereign country 1 India ... None None None None None None None None None MULTIPOLYGON (((77.80035 35.49541, 77.81533 35...
9 Admin-0 country 0 2 China CH1 1 2 Country 1 China ... None None None None None None None None None MULTIPOLYGON (((78.91769 33.38626, 78.91595 33...

10 rows × 169 columns

Each row contains the information for one country.

Each column is one property or variable.

Unlike pandas DataFrames, geopandas always must have a geometry column.

Let's plot this data

In [7]:
%matplotlib inline
fig, ax = plt.subplots(figsize=(15,10))
countries.plot(ax=ax)
ax.set_title("WGS84 (lat/lon)", fontdict={'fontsize':34})
Out[7]:
Text(0.5, 1.0, 'WGS84 (lat/lon)')
No description has been provided for this image

We can also get some additional information on this data. For example its projection

In [8]:
countries.crs
Out[8]:
<Geographic 2D CRS: EPSG:4326>
Name: WGS 84
Axis Info [ellipsoidal]:
- Lat[north]: Geodetic latitude (degree)
- Lon[east]: Geodetic longitude (degree)
Area of Use:
- name: World.
- bounds: (-180.0, -90.0, 180.0, 90.0)
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich

We can reproject the data from its current WGS84 projection to other ones. Let's do this and plot the results so we can see how different projections distort results.

In [9]:
fig, ax = plt.subplots(figsize=(15,10))
countries_merc = countries.to_crs(epsg=3857)
countries_merc.loc[countries_merc.NAME!='Antarctica'].reset_index().plot(ax=ax)
ax.set_title("Mercator", fontdict={'fontsize':34})
Out[9]:
Text(0.5, 1.0, 'Mercator')
No description has been provided for this image
In [10]:
countries_merc.crs
Out[10]:
<Projected CRS: EPSG:3857>
Name: WGS 84 / Pseudo-Mercator
Axis Info [cartesian]:
- X[east]: Easting (metre)
- Y[north]: Northing (metre)
Area of Use:
- name: World between 85.06°S and 85.06°N.
- bounds: (-180.0, -85.06, 180.0, 85.06)
Coordinate Operation:
- name: Popular Visualisation Pseudo-Mercator
- method: Popular Visualisation Pseudo Mercator
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich
In [11]:
cea = {'datum': 'WGS84',
 'lat_ts': 0,
 'lon_0': 0,
 'no_defs': True,
 'over': True,
 'proj': 'cea',
 'units': 'm',
 'x_0': 0,
 'y_0': 0}

cea = 'ESRI:54034'
fig, ax = plt.subplots(figsize=(15,10))
countries_cea = countries.to_crs(crs=cea)
countries_cea.plot(ax=ax)
ax.set_title("Cylindrical Equal Area", fontdict={'fontsize':34})
Out[11]:
Text(0.5, 1.0, 'Cylindrical Equal Area')
No description has been provided for this image
In [12]:
countries_cea.crs
Out[12]:
<Projected CRS: ESRI:54034>
Name: World_Cylindrical_Equal_Area
Axis Info [cartesian]:
- E[east]: Easting (metre)
- N[north]: Northing (metre)
Area of Use:
- name: World.
- bounds: (-180.0, -90.0, 180.0, 90.0)
Coordinate Operation:
- name: World_Cylindrical_Equal_Area
- method: Lambert Cylindrical Equal Area
Datum: World Geodetic System 1984
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich

Notice that each projection shows the world in a very different manner, distoring areas, distances etc. So you need to take care when doing computations to use the correct projection. An important issue to remember is that you need a projected (not geographical) projection to compute areas and distances. Let's compare these three a bit. Start with the boundaries of each.

In [13]:
print('[xmin, ymin, xmax, ymax] in three projections')
print(countries.total_bounds)
print(countries_merc.total_bounds)
print(countries_cea.total_bounds)

[xmin, ymin, xmax, ymax] in three projections
[-180.          -90.          180.           83.63410065]
[-2.00375083e+07 -2.25045148e+08  2.00375083e+07  1.84289200e+07]
[-20037508.34278923  -6363885.33192604  20037508.34278924
   6324296.52646162]

Let's describe the areas of these countries in the three projections

In [14]:
print('Area distribution in WGS84')
print(countries.area.describe(), '\n')

Area distribution in WGS84
count     258.000000
mean       83.053683
std       443.786684
min         0.000001
25%         0.065859
50%         5.857276
75%        37.279026
max      6049.574693
dtype: float64 


/var/folders/2r/7vb_23y1427bffj2wbz7mxfc0000gq/T/ipykernel_69226/1371744286.py:2: UserWarning: Geometry is in a geographic CRS. Results from 'area' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.

  print(countries.area.describe(), '\n')
In [15]:
print('Area distribution in Mercator')
print(countries_merc.area.describe(), '\n')

Area distribution in Mercator
count    2.580000e+02
mean     3.423154e+13
std      5.295922e+14
min      2.204709e+04
25%      9.801617e+08
50%      8.692411e+10
75%      5.411109e+11
max      8.507102e+15
dtype: float64
In [16]:
print('Area distribution in CEA')
print(countries_cea.area.describe(), '\n')

Area distribution in CEA
count    2.580000e+02
mean     5.690945e+11
std      1.826917e+12
min      1.220383e+04
25%      6.986665e+08
50%      5.148888e+10
75%      3.544773e+11
max      1.698019e+13
dtype: float64
In [17]:
countries['geometry']
Out[17]:
0      MULTIPOLYGON (((117.70361 4.16341, 117.70361 4...
1      MULTIPOLYGON (((117.70361 4.16341, 117.69711 4...
2      MULTIPOLYGON (((-69.51009 -17.50659, -69.50611...
3      POLYGON ((-69.51009 -17.50659, -69.51009 -17.5...
4      MULTIPOLYGON (((-69.51009 -17.50659, -69.63832...
                             ...                        
253    MULTIPOLYGON (((113.55860 22.16303, 113.56943 ...
254    POLYGON ((123.59702 -12.42832, 123.59775 -12.4...
255    POLYGON ((-79.98929 15.79495, -79.98782 15.796...
256    POLYGON ((-78.63707 15.86209, -78.64041 15.864...
257    POLYGON ((117.75389 15.15437, 117.75569 15.151...
Name: geometry, Length: 258, dtype: geometry
In [18]:
Point((0,0))
Out[18]:
No description has been provided for this image
In [19]:
Polygon(((0,0), (1,2), (3,0)))
Out[19]:
No description has been provided for this image

Let's compare the area of each country in the two projected projections

In [20]:
countries_merc = countries_merc.set_index('ADM0_A3')
countries_cea = countries_cea.set_index('ADM0_A3')
countries_merc['ratio_area'] = countries_merc.area / countries_cea.area
countries_cea['ratio_area'] = countries_merc.area / countries_cea.area
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.set_context("talk")
fig, ax = plt.subplots()
sns.scatterplot(x=countries_cea.area/1e6, y=countries_merc.area/1e6, ax=ax)
sns.lineplot(x=countries_cea.area/1e6, y=countries_cea.area/1e6, color='r', ax=ax)
ax.set_ylabel('Mercator')
ax.set_xlabel('CEA')
ax.set_title("Areas")
Out[20]:
Text(0.5, 1.0, 'Areas')
No description has been provided for this image

Now, how do we know what is correct? Let's get some data from WDI to compare the areas of countries in these projections to what the correct area should be (notice that each country usually will use a local projection that ensures areas are correctly computed, so their data should be closer to the truth than any of our global ones).

Here we use some of what we learned before in this notebook.

In [21]:
from pandas_datareader import data, wb
wbcountries = wb.get_countries()
wbcountries['name'] = wbcountries.name.str.strip()
wdi = wb.download(indicator=['AG.LND.TOTL.K2'], country=wbcountries.iso2c.values, start=2017, end=2017)
wdi.columns = ['WDI_area']
wdi = wdi.reset_index()
wdi = wdi.merge(wbcountries[['iso3c', 'iso2c', 'name']], left_on='country', right_on='name')

countries_cea['CEA_area'] = countries_cea.area / 1e6
countries_merc['MERC_area'] = countries_merc.area / 1e6
areas = pd.merge(countries_cea['CEA_area'], countries_merc['MERC_area'], left_index=True, right_index=True)

/Users/ozak/miniforge3/envs/GeoPython311env/lib/python3.11/site-packages/pandas_datareader/wb.py:592: UserWarning: Non-standard ISO country codes: 1A, 1W, 4E, 6F, 6N, 6X, 7E, 8S, A4, A5, A9, B1, B2, B3, B4, B6, B7, B8, C4, C5, C6, C7, C8, C9, D2, D3, D4, D5, D6, D7, EU, F1, F6, JG, M1, M2, N6, OE, R6, S1, S2, S3, S4, T2, T3, T4, T5, T6, T7, V1, V2, V3, V4, XC, XD, XE, XF, XG, XH, XI, XJ, XK, XL, XM, XN, XO, XP, XQ, XT, XU, XY, Z4, Z7, ZB, ZF, ZG, ZH, ZI, ZJ, ZQ, ZT
  warnings.warn(
/var/folders/2r/7vb_23y1427bffj2wbz7mxfc0000gq/T/ipykernel_69226/2997326858.py:4: FutureWarning: errors='ignore' is deprecated and will raise in a future version. Use to_numeric without passing `errors` and catch exceptions explicitly instead
  wdi = wb.download(indicator=['AG.LND.TOTL.K2'], country=wbcountries.iso2c.values, start=2017, end=2017)

Let's merge the WDI data with what we have computed before.

In [22]:
wdi = wdi.merge(areas, left_on='iso3c', right_index=True)
wdi
Out[22]:
country year WDI_area iso3c iso2c name CEA_area MERC_area
0 Aruba 2017 180.0 ABW AW Aruba 1.697662e+02 1.792215e+02
2 Afghanistan 2017 652230.0 AFG AF Afghanistan 6.421811e+05 9.349973e+05
4 Angola 2017 1246700.0 AGO AO Angola 1.244652e+06 1.316011e+06
5 Albania 2017 27400.0 ALB AL Albania 2.833579e+04 5.002434e+04
6 Andorra 2017 470.0 AND AD Andorra 4.522394e+02 8.335608e+02
... ... ... ... ... ... ... ... ...
260 Samoa 2017 2780.0 WSM WS Samoa 2.780425e+03 2.964662e+03
262 Yemen, Rep. 2017 527970.0 YEM YE Yemen, Rep. 4.530748e+05 4.929999e+05
263 South Africa 2017 1213090.0 ZAF ZA South Africa 1.219825e+06 1.605941e+06
264 Zambia 2017 743390.0 ZMB ZM Zambia 7.519143e+05 8.011173e+05
265 Zimbabwe 2017 386850.0 ZWE ZW Zimbabwe 3.893382e+05 4.382042e+05

213 rows × 8 columns

How correlated are these measures?

In [23]:
wdi.corr(numeric_only=True)
Out[23]:
WDI_area CEA_area MERC_area
WDI_area 1.000000 0.997195 0.822258
CEA_area 0.997195 1.000000 0.852868
MERC_area 0.822258 0.852868 1.000000

Let's change the shape of the data so we can plot it using seaborn.

In [24]:
wdi2 = wdi.melt(id_vars=['iso3c', 'iso2c', 'name', 'country', 'year', 'WDI_area'], value_vars=['CEA_area', 'MERC_area'])
wdi2
Out[24]:
iso3c iso2c name country year WDI_area variable value
0 ABW AW Aruba Aruba 2017 180.0 CEA_area 1.697662e+02
1 AFG AF Afghanistan Afghanistan 2017 652230.0 CEA_area 6.421811e+05
2 AGO AO Angola Angola 2017 1246700.0 CEA_area 1.244652e+06
3 ALB AL Albania Albania 2017 27400.0 CEA_area 2.833579e+04
4 AND AD Andorra Andorra 2017 470.0 CEA_area 4.522394e+02
... ... ... ... ... ... ... ... ...
421 WSM WS Samoa Samoa 2017 2780.0 MERC_area 2.964662e+03
422 YEM YE Yemen, Rep. Yemen, Rep. 2017 527970.0 MERC_area 4.929999e+05
423 ZAF ZA South Africa South Africa 2017 1213090.0 MERC_area 1.605941e+06
424 ZMB ZM Zambia Zambia 2017 743390.0 MERC_area 8.011173e+05
425 ZWE ZW Zimbabwe Zimbabwe 2017 386850.0 MERC_area 4.382042e+05

426 rows × 8 columns

In [25]:
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.set_context("talk")
fig, ax = plt.subplots()
sns.scatterplot(x='WDI_area', y='value', data=wdi2, hue='variable', ax=ax)
#sns.scatterplot(x='WDI_area', y='MERC_area', data=wdi, ax=ax)
sns.lineplot(x='WDI_area', y='WDI_area', data=wdi, color='r', ax=ax)
ax.set_ylabel('Other')
ax.set_xlabel('WDI')
ax.set_title("Areas")
ax.legend()
Out[25]:
<matplotlib.legend.Legend at 0x143adbc90>
No description has been provided for this image

We could use other data to compare, e.g. data from the CIA Factbook.

In [26]:
cia_area = pd.read_csv('https://web.archive.org/web/20201116182145if_/https://www.cia.gov/LIBRARY/publications/the-world-factbook/rankorder/rawdata_2147.txt', sep='\t', header=None)
cia_area = pd.DataFrame(cia_area[0].str.strip().str.split('\s\s+').tolist(), columns=['id', 'Name', 'area'])
cia_area.area = cia_area.area.str.replace(',', '').astype(int)
cia_area
Out[26]:
id Name area
0 1 Russia 17098242
1 2 Antarctica 14000000
2 3 Canada 9984670
3 4 United States 9833517
4 5 China 9596960
... ... ... ...
249 250 Spratly Islands 5
250 251 Ashmore and Cartier Islands 5
251 252 Coral Sea Islands 3
252 253 Monaco 2
253 254 Holy See (Vatican City) 0

254 rows × 3 columns

In [27]:
print('CEA area for Russia', countries_cea.area.loc['RUS'] / 1e6)
print('MERC area for Russia', countries_merc.area.loc['RUS'] / 1e6)
print('WDI area for Russia', wdi.loc[wdi.iso3c=='RUS', 'WDI_area'])
print('CIA area for Russia', cia_area.loc[cia_area.Name=='Russia', 'area'])

CEA area for Russia 16980189.52844945
MERC area for Russia 82997412.6652339
WDI area for Russia 202    16376870.0
Name: WDI_area, dtype: float64
CIA area for Russia 0    17098242
Name: area, dtype: int64

Again very similar result. CEA is closest to both WDI and CIA.

Exercise¶

  1. Merge the CIA data with the wdi data. You need to get correct codes for the countries to allow for the merge or correct the names to ensure they are compatible.
  2. Change the dataframe as we did with wdi2 and plot the association between these measures

Mapping data¶

Let's use the geoplot package to plot data in a map. As usual we can do it in many ways, but geoplot makes our life very easy. Let's import the various packages we will use.

In [28]:
import geoplot as gplt
import geoplot.crs as gcrs
import mapclassify as mc
import textwrap

Let's import some of the data we had downloaded before. Specifically, let's import the Penn World Tables data.

In [29]:
pwt = pd.read_stata(pathout + 'pwt.dta')
pwt_xls = pd.read_excel(pathout + 'pwt.xlsx')
pwt
Out[29]:
countrycode country currency_unit year rgdpe rgdpo pop emp avh hc ... csh_x csh_m csh_r pl_c pl_i pl_g pl_x pl_m pl_n pl_k
0 ABW Aruba Aruban Guilder 1950 NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 ABW Aruba Aruban Guilder 1951 NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 ABW Aruba Aruban Guilder 1952 NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 ABW Aruba Aruban Guilder 1953 NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4 ABW Aruba Aruban Guilder 1954 NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
12805 ZWE Zimbabwe US Dollar 2015 40141.617188 39798.644531 13.814629 6.393752 NaN 2.584653 ... 0.140172 -0.287693 -0.051930 0.479228 0.651287 0.541446 0.616689 0.533235 0.425715 1.778124
12806 ZWE Zimbabwe US Dollar 2016 41875.203125 40963.191406 14.030331 6.504374 NaN 2.616257 ... 0.131920 -0.251232 -0.016258 0.470640 0.651027 0.539631 0.619789 0.519718 0.419446 1.728804
12807 ZWE Zimbabwe US Dollar 2017 44672.175781 44316.742188 14.236595 6.611773 NaN 2.648248 ... 0.126722 -0.202827 -0.039897 0.473560 0.639560 0.519956 0.619739 0.552042 0.418681 1.756007
12808 ZWE Zimbabwe US Dollar 2018 44325.109375 43420.898438 14.438802 6.714952 NaN 2.680630 ... 0.144485 -0.263658 -0.020791 0.543757 0.655473 0.529867 0.641361 0.561526 0.426527 1.830088
12809 ZWE Zimbabwe US Dollar 2019 42296.062500 40826.570312 14.645468 6.831017 NaN 2.713408 ... 0.213562 -0.270959 -0.089798 0.494755 0.652439 0.500927 0.487763 0.430082 0.419883 1.580885

12810 rows × 52 columns

Let's recreate GDPpc data

In [30]:
# Get columns with GDP measures
gdpcols = pwt_xls.loc[pwt_xls['Variable definition'].apply(lambda x: str(x).upper().find('REAL GDP')!=-1), 'Variable name'].tolist()

# Generate GDPpc for each measure
for gdp in gdpcols:
    pwt[gdp + '_pc'] = pwt[gdp] / pwt['pop']

# GDPpc data
gdppccols = [col+'_pc' for col in gdpcols]
pwt[['countrycode', 'country', 'year'] + gdppccols]
Out[30]:
countrycode country year rgdpe_pc rgdpo_pc cgdpe_pc cgdpo_pc rgdpna_pc
0 ABW Aruba 1950 NaN NaN NaN NaN NaN
1 ABW Aruba 1951 NaN NaN NaN NaN NaN
2 ABW Aruba 1952 NaN NaN NaN NaN NaN
3 ABW Aruba 1953 NaN NaN NaN NaN NaN
4 ABW Aruba 1954 NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ...
12805 ZWE Zimbabwe 2015 2905.732553 2880.905780 2892.674328 2856.095690 3040.848887
12806 ZWE Zimbabwe 2016 2984.619759 2919.616893 2970.770578 2912.558803 3016.730437
12807 ZWE Zimbabwe 2017 3137.841301 3112.875107 3137.841301 3112.875107 3112.875107
12808 ZWE Zimbabwe 2018 3069.860600 3007.236919 3071.061791 3017.391036 3217.517468
12809 ZWE Zimbabwe 2019 2887.996649 2787.658975 2889.980517 2805.080907 2915.172824

12810 rows × 8 columns

Let's map GDPpc for the year 2010 using geoplot. For this, let's write two functions that will simplify plotting and saving maps. Also, we can reuse it whenever we need to create a new map for the world.

In [31]:
# Functions for plotting
def center_wrap(text, cwidth=32, **kw):
    '''Center Text (to be used in legend)'''
    lines = text
    #lines = textwrap.wrap(text, **kw)
    return "\n".join(line.center(cwidth) for line in lines)

def MyChoropleth(mydf=pwt.loc[pwt.year==2010], myfile='GDPpc2010', myvar='rgdpe_pc',
                  mylegend='GDP per capita 2010',
                  k=5,
                  extent=[-180, -90, 180, 90],
                  bbox_to_anchor=(0.2, 0.5),
                  edgecolor='white', facecolor='lightgray',
                  scheme='FisherJenks',
                  save=True,
                  percent=False,
                  **kwargs):
    # Chloropleth
    # Color scheme
    if scheme=='EqualInterval':
        scheme = mc.EqualInterval(mydf[myvar], k=k)
    elif scheme=='Quantiles':
        scheme = mc.Quantiles(mydf[myvar], k=k)
    elif scheme=='BoxPlot':
        scheme = mc.BoxPlot(mydf[myvar], k=k)
    elif scheme=='FisherJenks':
        scheme = mc.FisherJenks(mydf[myvar], k=k)
    elif scheme=='FisherJenksSampled':
        scheme = mc.FisherJenksSampled(mydf[myvar], k=k)
    elif scheme=='HeadTailBreaks':
        scheme = mc.HeadTailBreaks(mydf[myvar], k=k)
    elif scheme=='JenksCaspall':
        scheme = mc.JenksCaspall(mydf[myvar], k=k)
    elif scheme=='JenksCaspallForced':
        scheme = mc.JenksCaspallForced(mydf[myvar], k=k)
    elif scheme=='JenksCaspallSampled':
        scheme = mc.JenksCaspallSampled(mydf[myvar], k=k)
    elif scheme=='KClassifiers':
        scheme = mc.KClassifiers(mydf[myvar], k=k)
    # Format legend
    upper_bounds = scheme.bins
    # get and format all bounds
    bounds = []
    for index, upper_bound in enumerate(upper_bounds):
        if index == 0:
            lower_bound = mydf[myvar].min()
        else:
            lower_bound = upper_bounds[index-1]
        # format the numerical legend here
        if percent:
            bound = f'{lower_bound:.0%} - {upper_bound:.0%}'
        else:
            bound = f'{float(lower_bound):,.0f} - {float(upper_bound):,.0f}'
        bounds.append(bound)
    legend_labels = bounds
    #Plot
    ax = gplt.choropleth(
        mydf, hue=myvar, projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
        edgecolor='white', linewidth=1,
        cmap='Reds', legend=True,
        scheme=scheme,
        legend_kwargs={'bbox_to_anchor': bbox_to_anchor,
                       'frameon': True,
                       'title':mylegend,
                       },
        legend_labels = legend_labels,
        figsize=(24, 16),
        rasterized=True,
    )
    gplt.polyplot(
        countries, projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
        edgecolor=edgecolor, facecolor=facecolor,
        ax=ax,
        rasterized=True,
        extent=extent,
    )
    if save:
        plt.savefig(pathgraphs + myfile + '_' + myvar +'.pdf', dpi=300, bbox_inches='tight')
        plt.savefig(pathgraphs + myfile + '_' + myvar +'.png', dpi=300, bbox_inches='tight')
    pass

Let's merge the PWT GDPpc data with our shape file.

In [32]:
year = 2010
gdppc = pwt.loc[pwt.year==year].reset_index(drop=True).copy()
gdppc = countries.merge(gdppc, left_on='ADM0_A3', right_on='countrycode')
gdppc = gdppc.dropna(subset=['rgdpe_pc'])
mylegend = center_wrap(["GDP per capita in " + str(year)], cwidth=32, width=32)
MyChoropleth(mydf=gdppc, myfile='PWT_GDP_' + str(year), myvar='rgdpe_pc', mylegend=mylegend, k=10, scheme='Quantiles', save=True)
No description has been provided for this image
In [33]:
year = 2000
gdppc = pwt.loc[pwt.year==year].reset_index(drop=True).copy()
gdppc = countries.merge(gdppc, left_on='ADM0_A3', right_on='countrycode')
gdppc = gdppc.dropna(subset=['rgdpe_pc'])
mylegend = center_wrap(["GDP per capita in " + str(year)], cwidth=32, width=32)
MyChoropleth(mydf=gdppc, myfile='PWT_GDP_' + str(year), myvar='rgdpe_pc', mylegend=mylegend, k=10, scheme='Quantiles', save=True)
No description has been provided for this image
In [34]:
year = 2000
gdppc = pwt.loc[pwt.year==year].reset_index(drop=True).copy()
gdppc = countries.merge(gdppc, left_on='ADM0_A3', right_on='countrycode')
gdppc = gdppc.dropna(subset=['pop'])
mylegend = center_wrap(["Population in " + str(year)], cwidth=32, width=32)
MyChoropleth(mydf=gdppc, myfile='PWT_POP_' + str(year), myvar='pop', mylegend=mylegend, k=10, scheme='Quantiles', save=True)
No description has been provided for this image

GIS operations, functions and properties¶

Let's explore the data with some of the functions of geopandas.

Let's start by finding the centroid of every country and plot it.

In [35]:
centroids = countries.copy()
centroids.geometry = centroids.centroid
ax = gplt.pointplot(
    centroids, projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
    figsize=(24, 16),
    rasterized=True,
)
gplt.polyplot(countries.geometry, projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
              edgecolor='white', facecolor='lightgray',
              extent=[-180, -90, 180, 90],
              ax=ax)

/var/folders/2r/7vb_23y1427bffj2wbz7mxfc0000gq/T/ipykernel_69226/1290617103.py:2: UserWarning: Geometry is in a geographic CRS. Results from 'centroid' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.

  centroids.geometry = centroids.centroid
Out[35]:
<GeoAxes: >
No description has been provided for this image
In [36]:
centroids.to_file(pathout + 'centroids.shp')
In [37]:
centroids.loc[centroids.SOVEREIGNT=='Southern Patagonian Ice Field']
Out[37]:
featurecla scalerank LABELRANK SOVEREIGNT SOV_A3 ADM0_DIF LEVEL TYPE TLC ADMIN ... FCLASS_TR FCLASS_ID FCLASS_PL FCLASS_GR FCLASS_IT FCLASS_NL FCLASS_SE FCLASS_BD FCLASS_UA geometry
173 Admin-0 country 0 9 Southern Patagonian Ice Field SPI 0 2 Indeterminate None Southern Patagonian Ice Field ... Unrecognized Unrecognized Unrecognized Unrecognized None None None Unrecognized Unrecognized POINT (-73.31883 -49.51234)

1 rows × 169 columns

Let's compute distances between the centroids.¶

For this we will use the geopy package.¶

In [38]:
from geopy.distance import geodesic, great_circle
import itertools
centroids['xy'] = centroids.geometry.apply(lambda x: [x.y, x.x])
In [39]:
mypairs = pd.DataFrame(index = pd.MultiIndex.from_arrays(
                    np.array([x for x in itertools.product(centroids['ADM0_A3'].tolist(), repeat=2)]).T,
                    names = ['country_1','country_2'])).reset_index()
mypairs = mypairs.merge(centroids[['ADM0_A3', 'xy']], left_on='country_1', right_on='ADM0_A3')
mypairs = mypairs.merge(centroids[['ADM0_A3', 'xy']], left_on='country_2', right_on='ADM0_A3', suffixes=['_1', '_2'])
mypairs
Out[39]:
country_1 country_2 ADM0_A3_1 xy_1 ADM0_A3_2 xy_2
0 IDN IDN IDN [-2.222961002517387, 117.2704333391668] IDN [-2.222961002517387, 117.2704333391668]
1 IDN MYS IDN [-2.222961002517387, 117.2704333391668] MYS [3.7923928509530205, 109.6988684421668]
2 IDN CHL IDN [-2.222961002517387, 117.2704333391668] CHL [-37.74360663523242, -71.36437476479367]
3 IDN BOL IDN [-2.222961002517387, 117.2704333391668] BOL [-16.7068768105592, -64.68475372880839]
4 IDN PER IDN [-2.222961002517387, 117.2704333391668] PER [-9.154388480752162, -74.37806457210715]
... ... ... ... ... ... ...
66559 SCR MAC SCR [15.152112822000067, 117.75381196333339] MAC [22.157784411664835, 113.55019787171386]
66560 SCR ATC SCR [15.152112822000067, 117.75381196333339] ATC [-12.432577176848286, 123.58636778644266]
66561 SCR BJN SCR [15.152112822000067, 117.75381196333339] BJN [15.795009963377407, -79.9878658593175]
66562 SCR SER SCR [15.152112822000067, 117.75381196333339] SER [15.864460896333414, -78.63811872766658]
66563 SCR SCR SCR [15.152112822000067, 117.75381196333339] SCR [15.152112822000067, 117.75381196333339]

66564 rows × 6 columns

In [40]:
mypairs['geodesic_dist'] = mypairs.apply(lambda x: geodesic(x.xy_1, x.xy_2).km, axis=1)
mypairs['great_circle_dist'] = mypairs.apply(lambda x: great_circle(x.xy_1, x.xy_2).km, axis=1)
mypairs
Out[40]:
country_1 country_2 ADM0_A3_1 xy_1 ADM0_A3_2 xy_2 geodesic_dist great_circle_dist
0 IDN IDN IDN [-2.222961002517387, 117.2704333391668] IDN [-2.222961002517387, 117.2704333391668] 0.000000 0.000000
1 IDN MYS IDN [-2.222961002517387, 117.2704333391668] MYS [3.7923928509530205, 109.6988684421668] 1073.341454 1074.915491
2 IDN CHL IDN [-2.222961002517387, 117.2704333391668] CHL [-37.74360663523242, -71.36437476479367] 15491.447867 15482.921743
3 IDN BOL IDN [-2.222961002517387, 117.2704333391668] BOL [-16.7068768105592, -64.68475372880839] 17899.591177 17899.294953
4 IDN PER IDN [-2.222961002517387, 117.2704333391668] PER [-9.154388480752162, -74.37806457210715] 18217.220296 18207.778329
... ... ... ... ... ... ... ... ...
66559 SCR MAC SCR [15.152112822000067, 117.75381196333339] MAC [22.157784411664835, 113.55019787171386] 893.134905 895.894217
66560 SCR ATC SCR [15.152112822000067, 117.75381196333339] ATC [-12.432577176848286, 123.58636778644266] 3117.742839 3133.757085
66561 SCR BJN SCR [15.152112822000067, 117.75381196333339] BJN [15.795009963377407, -79.9878658593175] 16072.183081 16060.602969
66562 SCR SER SCR [15.152112822000067, 117.75381196333339] SER [15.864460896333414, -78.63811872766658] 16135.829664 16124.702173
66563 SCR SCR SCR [15.152112822000067, 117.75381196333339] SCR [15.152112822000067, 117.75381196333339] 0.000000 0.000000

66564 rows × 8 columns

In [41]:
mypairs.corr(numeric_only=True)
Out[41]:
geodesic_dist great_circle_dist
geodesic_dist 1.000000 0.999997
great_circle_dist 0.999997 1.000000

Let's now use the cylindrical equal area projection and geopandas distance function to compute the distance between centroids.

In [42]:
centroids_cea = countries_cea.copy()
centroids_cea.reset_index(inplace=True)
centroids_cea.geometry = centroids_cea.centroid
centroids_cea['xy'] = centroids_cea.geometry.apply(lambda x: [x.y, x.x])
mypairs_cea = pd.DataFrame(index = pd.MultiIndex.from_arrays(
                    np.array([x for x in itertools.product(centroids_cea['ADM0_A3'].tolist(), repeat=2)]).T,
                    names = ['country_1','country_2'])).reset_index()
mypairs_cea = mypairs_cea.merge(centroids_cea[['ADM0_A3', 'geometry', 'xy']], left_on='country_1', right_on='ADM0_A3')
mypairs_cea = mypairs_cea.merge(centroids_cea[['ADM0_A3', 'geometry', 'xy']], left_on='country_2', right_on='ADM0_A3', suffixes=['_1', '_2'])
In [43]:
mypairs_cea
Out[43]:
country_1 country_2 ADM0_A3_1 geometry_1 xy_1 ADM0_A3_2 geometry_2 xy_2
0 IDN IDN IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316]
1 IDN MYS IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] MYS POINT (12211550.168 418637.642) [418637.64215854264, 12211550.16769715]
2 IDN CHL IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] CHL POINT (-7927268.774 -3670204.431) [-3670204.4310664986, -7927268.774365294]
3 IDN BOL IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] BOL POINT (-7201342.481 -1814919.515) [-1814919.5145804614, -7201342.480506779]
4 IDN PER IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] PER POINT (-8281824.471 -999164.638) [-999164.6380899184, -8281824.47083905]
... ... ... ... ... ... ... ... ...
66559 SCR MAC SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] MAC POINT (12640350.411 2390981.940) [2390981.9398800945, 12640350.411234612]
66560 SCR ATC SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] ATC POINT (13757571.530 -1364242.801) [-1364242.8007381177, 13757571.529629346]
66561 SCR BJN SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] BJN POINT (-8904208.497 1725054.531) [1725054.5313122338, -8904208.497110264]
66562 SCR SER SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] SER POINT (-8753955.334 1732450.150) [1732450.1498870007, -8753955.333704835]
66563 SCR SCR SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157]

66564 rows × 8 columns

In [44]:
mypairs_cea['CEA_dist'] = mypairs_cea.apply(lambda x: x.geometry_1.distance(x.geometry_2)/1e3, axis=1)
mypairs_cea
Out[44]:
country_1 country_2 ADM0_A3_1 geometry_1 xy_1 ADM0_A3_2 geometry_2 xy_2 CEA_dist
0 IDN IDN IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] 0.000000
1 IDN MYS IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] MYS POINT (12211550.168 418637.642) [418637.64215854264, 12211550.16769715] 1071.733796
2 IDN CHL IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] CHL POINT (-7927268.774 -3670204.431) [-3670204.4310664986, -7927268.774365294] 21258.681949
3 IDN BOL IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] BOL POINT (-7201342.481 -1814919.515) [-1814919.5145804614, -7201342.480506779] 20315.704573
4 IDN PER IDN POINT (13053566.271 -244402.485) [-244402.48450644588, 13053566.27147316] PER POINT (-8281824.471 -999164.638) [-999164.6380899184, -8281824.47083905] 21348.736825
... ... ... ... ... ... ... ... ... ...
66559 SCR MAC SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] MAC POINT (12640350.411 2390981.940) [2390981.9398800945, 12640350.411234612] 870.900172
66560 SCR ATC SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] ATC POINT (13757571.530 -1364242.801) [-1364242.8007381177, 13757571.529629346] 3089.711474
66561 SCR BJN SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] BJN POINT (-8904208.497 1725054.531) [1725054.5313122338, -8904208.497110264] 22012.609702
66562 SCR SER SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] SER POINT (-8753955.334 1732450.150) [1732450.1498870007, -8753955.333704835] 21862.381722
66563 SCR SCR SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] SCR POINT (13108294.387 1656478.335) [1656478.33538606, 13108294.386725157] 0.000000

66564 rows × 9 columns

Let's merge the three distance measures and see how similar they are.

In [45]:
dists = mypairs[['country_1', 'country_2', 'geodesic_dist', 'great_circle_dist']].copy()
dists = dists.merge(mypairs_cea[['country_1', 'country_2', 'CEA_dist']])
dists
Out[45]:
country_1 country_2 geodesic_dist great_circle_dist CEA_dist
0 IDN IDN 0.000000 0.000000 0.000000
1 IDN MYS 1073.341454 1074.915491 1071.733796
2 IDN CHL 15491.447867 15482.921743 21258.681949
3 IDN BOL 17899.591177 17899.294953 20315.704573
4 IDN PER 18217.220296 18207.778329 21348.736825
... ... ... ... ... ...
66559 SCR MAC 893.134905 895.894217 870.900172
66560 SCR ATC 3117.742839 3133.757085 3089.711474
66561 SCR BJN 16072.183081 16060.602969 22012.609702
66562 SCR SER 16135.829664 16124.702173 21862.381722
66563 SCR SCR 0.000000 0.000000 0.000000

66564 rows × 5 columns

In [46]:
dists.corr(numeric_only=True)
Out[46]:
geodesic_dist great_circle_dist CEA_dist
geodesic_dist 1.000000 0.999997 0.855468
great_circle_dist 0.999997 1.000000 0.855163
CEA_dist 0.855468 0.855163 1.000000
In [47]:
centroids_merc = countries_merc.copy()
centroids_merc.reset_index(inplace=True)
centroids_merc.geometry = centroids_merc.centroid
centroids_merc['xy'] = centroids_merc.geometry.apply(lambda x: [x.y, x.x])
mypairs_merc = pd.DataFrame(index = pd.MultiIndex.from_arrays(
                    np.array([x for x in itertools.product(centroids_merc['ADM0_A3'].tolist(), repeat=2)]).T,
                    names = ['country_1','country_2'])).reset_index()
mypairs_merc = mypairs_merc.merge(centroids_merc[['ADM0_A3', 'geometry', 'xy']], left_on='country_1', right_on='ADM0_A3')
mypairs_merc = mypairs_merc.merge(centroids_merc[['ADM0_A3', 'geometry', 'xy']], left_on='country_2', right_on='ADM0_A3', suffixes=['_1', '_2'])
In [48]:
mypairs_merc['MERC_dist'] = mypairs_merc.apply(lambda x: x.geometry_1.distance(x.geometry_2)/1e3, axis=1)
mypairs_merc
Out[48]:
country_1 country_2 ADM0_A3_1 geometry_1 xy_1 ADM0_A3_2 geometry_2 xy_2 MERC_dist
0 IDN IDN IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] 0.000000
1 IDN MYS IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] MYS POINT (12211696.493 422897.505) [422897.5049133076, 12211696.493171558] 1078.531213
2 IDN CHL IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] CHL POINT (-7959811.966 -4915458.954) [-4915458.9537708275, -7959811.965630335] 21527.123498
3 IDN BOL IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] BOL POINT (-7200010.945 -1894653.148) [-1894653.1483839012, -7200010.9452187605] 20322.189721
4 IDN PER IDN POINT (13055431.810 -248921.141) [-248921.14144190453, 13055431.809760388] PER POINT (-8277554.831 -1032942.536) [-1032942.5356006415, -8277554.83112532] 21347.388800
... ... ... ... ... ... ... ... ... ...
66559 SCR MAC SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] MAC POINT (12640349.997 2530481.032) [2530481.0318028885, 12640349.997044222] 947.378708
66560 SCR ATC SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] ATC POINT (13757571.532 -1394978.493) [-1394978.4931683333, 13757571.532360038] 3168.942872
66561 SCR BJN SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] BJN POINT (-8904208.497 1780995.890) [1780995.889639691, -8904208.497089265] 22012.628140
66562 SCR SER SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] SER POINT (-8753955.334 1789031.886) [1789031.8864233475, -8753955.333704833] 21862.404610
66563 SCR SCR SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] SCR POINT (13108294.387 1706736.857) [1706736.857093246, 13108294.386725157] 0.000000

66564 rows × 9 columns

In [49]:
dists = dists.merge(mypairs_merc[['country_1', 'country_2', 'MERC_dist']])
dists
Out[49]:
country_1 country_2 geodesic_dist great_circle_dist CEA_dist MERC_dist
0 IDN IDN 0.000000 0.000000 0.000000 0.000000
1 IDN MYS 1073.341454 1074.915491 1071.733796 1078.531213
2 IDN CHL 15491.447867 15482.921743 21258.681949 21527.123498
3 IDN BOL 17899.591177 17899.294953 20315.704573 20322.189721
4 IDN PER 18217.220296 18207.778329 21348.736825 21347.388800
... ... ... ... ... ... ...
66559 SCR MAC 893.134905 895.894217 870.900172 947.378708
66560 SCR ATC 3117.742839 3133.757085 3089.711474 3168.942872
66561 SCR BJN 16072.183081 16060.602969 22012.609702 22012.628140
66562 SCR SER 16135.829664 16124.702173 21862.381722 21862.404610
66563 SCR SCR 0.000000 0.000000 0.000000 0.000000

66564 rows × 6 columns

In [50]:
dists.corr(numeric_only=True)
Out[50]:
geodesic_dist great_circle_dist CEA_dist MERC_dist
geodesic_dist 1.000000 0.999997 0.855468 0.529885
great_circle_dist 0.999997 1.000000 0.855163 0.530099
CEA_dist 0.855468 0.855163 1.000000 0.573664
MERC_dist 0.529885 0.530099 0.573664 1.000000

Improving Centroids¶

One major issue with the centroids function we used is that it may not set the centroid inside the geometry. E.g., a country composed of islands may have its centroid at sea.¶

In [51]:
def largest_polygon_centroid(multipolygon):
    if multipolygon.geom_type == "Polygon":
        centroid = multipolygon.centroid
        if centroid.intersects(multipolygon)==False:
            centroid = multipolygon.representative_point()
        return centroid
    elif multipolygon.geom_type == "MultiPolygon":
        areas = np.array([polygon.area for polygon in multipolygon.geoms])
        largest_polygon = multipolygon.geoms[np.argmax(areas)]
        centroid = largest_polygon.centroid
        if centroid.intersects(largest_polygon)==False:
            centroid = largest_polygon.representative_point()
        return centroid
    
def largest_polygon_centroid_representative(multipolygon):
    if multipolygon.geom_type == "Polygon":
        centroid = multipolygon.representative_point()
        return centroid
    elif multipolygon.geom_type == "MultiPolygon":
        areas = np.array([polygon.area for polygon in multipolygon.geoms])
        largest_polygon = multipolygon.geoms[np.argmax(areas)]
        centroid = largest_polygon.representative_point()
        return centroid
In [52]:
# Largest polygon centroid
centroids_real = countries.copy()
centroids_real.geometry = centroids_real.geometry.apply(largest_polygon_centroid)

# Largest polygon representative point
centroids_repr = countries.copy()
centroids_repr.geometry = centroids_repr.geometry.apply(largest_polygon_centroid_representative)
In [53]:
ax = gplt.pointplot(centroids, 
                    projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
                    figsize=(24, 16),
                    rasterized=True,
)
gplt.pointplot(centroids_real, 
               projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
               rasterized=True,
               ax=ax,
               color='r'
)
gplt.pointplot(centroids_repr, 
               projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
               rasterized=True,
               ax=ax,
               color='g'
)
gplt.polyplot(countries.geometry, 
              projection=gcrs.PlateCarree(central_longitude=0.0, globe=None),
              edgecolor='white', facecolor='lightgray',
              extent=[-180, -90, 180, 90],
              ax=ax)
Out[53]:
<GeoAxes: >
No description has been provided for this image

Faster and easier distance computations¶

In [54]:
centroids_real_cea = centroids_real.to_crs(cea).set_index('ADM0_A3')
centroids_repr_cea = centroids_real.to_crs(cea).set_index('ADM0_A3')
In [55]:
%%time
dists_real_repr = centroids_real_cea.geometry.apply(lambda x: centroids_repr_cea.distance(x))

CPU times: user 16.9 ms, sys: 843 µs, total: 17.7 ms
Wall time: 16.8 ms
In [56]:
dists_real_repr = dists_real_repr.reset_index().melt(id_vars='ADM0_A3', value_name='distance')
dists_real_repr
Out[56]:
ADM0_A3 ADM0_A3 distance
0 IDN IDN 0.000000e+00
1 IDN IDN 4.278081e+05
2 IDN IDN 2.094563e+07
3 IDN IDN 1.997453e+07
4 IDN IDN 2.099543e+07
... ... ... ...
66559 SCR SCR 8.687421e+05
66560 SCR SCR 3.089711e+06
66561 SCR SCR 2.201261e+07
66562 SCR SCR 2.186238e+07
66563 SCR SCR 0.000000e+00

66564 rows × 3 columns

Spatial Joins and Overlays¶

Spatial Joins¶

A spatial join uses binary predicates such as intersects and crosses to combine two GeoDataFrames based on the spatial relationship between their geometries.

A common use case might be a spatial join between a point layer and a polygon layer where you want to retain the point geometries and grab the attributes of the intersecting polygons.

illustration

Types of spatial joins¶

Geopandas currently support the following methods of spatial joins. We refer to the left_df and right_df which are the correspond to the two dataframes passed in as args.

Left outer join¶

In a LEFT OUTER JOIN (how='left'), we keep all rows from the left and duplicate them if necessary to represent multiple hits between the two dataframes. We retain attributes of the right if they intersect and lose right rows that don't intersect. A left outer join implies that we are interested in retaining the geometries of the left.

Right outer join¶

In a RIGHT OUTER JOIN (how='right'), we keep all rows from the right and duplicate them if necessary to represent multiple hits between the two dataframes. We retain attributes of the left if they intersect and lose left rows that don't intersect. A right outer join implies that we are interested in retaining the geometries of the right.

Inner join¶

In an INNER JOIN (how='inner'), we keep rows from the right and left only where their binary predicate is True. We duplicate them if necessary to represent multiple hits between the two dataframes. We retain attributes of the right and left only if they intersect and lose all rows that do not. An inner join implies that we are interested in retaining the geometries of the left.

Example using Populated places¶

In [57]:
headers = {'User-Agent': 'Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/51.0.2704.103 Safari/537.36', 'Accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8'}

url = 'https://naturalearth.s3.amazonaws.com/10m_cultural/ne_10m_populated_places.zip'
r = requests.get(url, headers=headers)
populated_places = gp.read_file(io.BytesIO(r.content))
In [58]:
populated_places.head()
Out[58]:
SCALERANK NATSCALE LABELRANK FEATURECLA NAME NAMEPAR NAMEALT NAMEASCII ADM0CAP CAPIN ... FCLASS_ID FCLASS_PL FCLASS_GR FCLASS_IT FCLASS_NL FCLASS_SE FCLASS_BD FCLASS_UA FCLASS_TLC geometry
0 10 1 8.0 Admin-1 capital Colonia del Sacramento None None Colonia del Sacramento 0 None ... None None None None None None None None None POINT (-57.83612 -34.46979)
1 10 1 8.0 Admin-1 capital Trinidad None None Trinidad 0 None ... None None None None None None None None None POINT (-56.90100 -33.54400)
2 10 1 8.0 Admin-1 capital Fray Bentos None None Fray Bentos 0 None ... None None None None None None None None None POINT (-58.30400 -33.13900)
3 10 1 8.0 Admin-1 capital Canelones None None Canelones 0 None ... None None None None None None None None None POINT (-56.28400 -34.53800)
4 10 1 8.0 Admin-1 capital Florida None None Florida 0 None ... None None None None None None None None None POINT (-56.21500 -34.09900)

5 rows × 138 columns

Let's find the places located in each country and count how many there are¶

Since ADM0_A3 is available in both datasets so this is not really necessary, but we do it just to show the power of spatial joins¶

In [59]:
populated_places['ADM0_A3']
Out[59]:
0       URY
1       URY
2       URY
3       URY
4       URY
       ... 
7337    NZL
7338    NZL
7339    NZL
7340    IND
7341    IND
Name: ADM0_A3, Length: 7342, dtype: object

The number of places in each country is¶

In [60]:
number_pop_pl = populated_places.groupby(['ADM0_A3'])['geometry'].count()
number_pop_pl
Out[60]:
ADM0_A3
ABW     1
AFG    33
AGO    49
ALB    26
ALD     1
       ..
WSM     1
YEM    20
ZAF    72
ZMB    34
ZWE    20
Name: geometry, Length: 225, dtype: int64

Imagine we did not have ADM0_A3¶

In [61]:
populated_places_noadm = populated_places.copy().drop(columns = ['ADM0_A3'])
populated_places_noadm.head()
Out[61]:
SCALERANK NATSCALE LABELRANK FEATURECLA NAME NAMEPAR NAMEALT NAMEASCII ADM0CAP CAPIN ... FCLASS_ID FCLASS_PL FCLASS_GR FCLASS_IT FCLASS_NL FCLASS_SE FCLASS_BD FCLASS_UA FCLASS_TLC geometry
0 10 1 8.0 Admin-1 capital Colonia del Sacramento None None Colonia del Sacramento 0 None ... None None None None None None None None None POINT (-57.83612 -34.46979)
1 10 1 8.0 Admin-1 capital Trinidad None None Trinidad 0 None ... None None None None None None None None None POINT (-56.90100 -33.54400)
2 10 1 8.0 Admin-1 capital Fray Bentos None None Fray Bentos 0 None ... None None None None None None None None None POINT (-58.30400 -33.13900)
3 10 1 8.0 Admin-1 capital Canelones None None Canelones 0 None ... None None None None None None None None None POINT (-56.28400 -34.53800)
4 10 1 8.0 Admin-1 capital Florida None None Florida 0 None ... None None None None None None None None None POINT (-56.21500 -34.09900)

5 rows × 137 columns

How can we find the number of populated places in each country? Using spatial joins to identify which places are located in the country¶

Let's use gp.sjoin to get the the spatial join between both geodataframes¶

In [62]:
mysjoin = populated_places_noadm.sjoin(countries)
mysjoin
Out[62]:
SCALERANK NATSCALE LABELRANK_left FEATURECLA NAME_left NAMEPAR NAMEALT NAMEASCII ADM0CAP CAPIN ... FCLASS_VN_right FCLASS_TR_right FCLASS_ID_right FCLASS_PL_right FCLASS_GR_right FCLASS_IT_right FCLASS_NL_right FCLASS_SE_right FCLASS_BD_right FCLASS_UA_right
0 10 1 8.0 Admin-1 capital Colonia del Sacramento None None Colonia del Sacramento 0 None ... None None None None None None None None None None
1 10 1 8.0 Admin-1 capital Trinidad None None Trinidad 0 None ... None None None None None None None None None None
2 10 1 8.0 Admin-1 capital Fray Bentos None None Fray Bentos 0 None ... None None None None None None None None None None
3 10 1 8.0 Admin-1 capital Canelones None None Canelones 0 None ... None None None None None None None None None None
4 10 1 8.0 Admin-1 capital Florida None None Florida 0 None ... None None None None None None None None None None
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
7337 8 10 8.0 Populated place Cambridge None None Cambridge 0 None ... None None None None None None None None None None
7338 8 10 8.0 Populated place Kerikeri None None Kerikeri 0 None ... None None None None None None None None None None
7339 8 10 8.0 Populated place Turangi None None Turangi 0 None ... None None None None None None None None None None
7340 4 50 2.0 Admin-1 capital Leh None None Leh 0 None ... None None None None None None None None None None
7341 4 50 50.0 Admin-1 capital Amaravati None None Amaravati 0 None ... None None None None None None None None None None

7324 rows × 306 columns

sjoin by default uses the how=inner option¶

and keeps the geometries in the left dataframe¶

that intersect the right dataframe¶

We're not limited to using the intersection binary predicate. Any of the Shapely geometry methods that return a Boolean can be used by specifying the predicate kwarg.¶

You can change this to other options:¶

predicate='touches', or predicate='within', etc.¶

Let's compare results¶

In [63]:
mysjoin_pl = mysjoin.groupby(['ADM0_A3'])['geometry'].count()
mysjoin_pl
Out[63]:
ADM0_A3
ABW     1
AFG    33
AGO    48
ALB    26
ALD     1
       ..
WSM     1
YEM    20
ZAF    72
ZMB    34
ZWE    20
Name: geometry, Length: 225, dtype: int64
In [64]:
number_pop_pl
Out[64]:
ADM0_A3
ABW     1
AFG    33
AGO    49
ALB    26
ALD     1
       ..
WSM     1
YEM    20
ZAF    72
ZMB    34
ZWE    20
Name: geometry, Length: 225, dtype: int64
In [65]:
mysjoin_pl-number_pop_pl
Out[65]:
ADM0_A3
ABW    0.0
AFG    0.0
AGO   -1.0
ALB    0.0
ALD    0.0
      ... 
WSM    0.0
YEM    0.0
ZAF    0.0
ZMB    0.0
ZWE    0.0
Name: geometry, Length: 228, dtype: float64
In [66]:
compare_pl = pd.merge(mysjoin_pl, number_pop_pl, left_index=True, right_index=True, suffixes=['_sjoin', '_true'])
compare_pl
Out[66]:
geometry_sjoin geometry_true
ADM0_A3
ABW 1 1
AFG 33 33
AGO 48 49
ALB 26 26
ALD 1 1
... ... ...
WSM 1 1
YEM 20 20
ZAF 72 72
ZMB 34 34
ZWE 20 20

222 rows × 2 columns

Where are there differences?¶

In [67]:
compare_pl.loc[compare_pl['geometry_sjoin']!=compare_pl['geometry_true']]
Out[67]:
geometry_sjoin geometry_true
ADM0_A3
AGO 48 49
ARE 7 8
ARG 156 158
CAN 254 255
COL 71 72
CYP 3 4
DOM 30 31
GRL 16 22
KAZ 95 96
NAM 28 27
NOR 35 34
NZL 53 52
PAN 13 14
PER 87 89
PNG 22 23
PRT 23 24
USA 768 769

Exercise¶

Change predicate and how to ensure you get the correct result.¶

Overlays¶

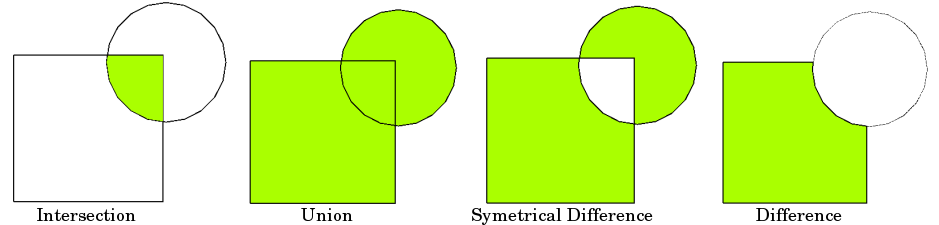
Spatial overlays allow you to compare two GeoDataFrames containing polygon or multipolygon geometries and create a new GeoDataFrame with the new geometries representing the spatial combination and merged properties. This allows you to answer questions like

How many people live within 100kms of a border and within 200kms of a populated place?

The basic idea is demonstrated by the graphic below but keep in mind that overlays operate at the dataframe level, not on individual geometries, and the properties from both are retained

illustration

Let us show how to answer the question above for one country, say Colombia¶

First, we need to get Colombia and its buffer¶

In [68]:
col = countries.loc[countries['ADM0_A3']=='COL'].reset_index(drop=True)
col = col.to_crs(cea)

We convert to CEA because we want to construct buffers around the border¶

In [69]:
col_buffer = col.copy()
col_buffer.geometry = col_buffer.boundary.buffer(100 * 1e3)
col_buffer.plot()
Out[69]:
<Axes: >
No description has been provided for this image

Now, let's select populated places in Colombia¶

In [73]:
col_places = populated_places.loc[populated_places['ADM0_A3']=='COL'].reset_index()
col_places = col_places.to_crs(cea)
col_places.plot()
Out[73]:
<Axes: >
No description has been provided for this image
In [75]:
col_places_buffer = col_places.copy()
col_places_buffer.geometry = col_places_buffer.buffer(200 * 1e3)
col_places_buffer.plot()
Out[75]:
<Axes: >
No description has been provided for this image

To find the number of people within 100kms of a border and 200kms of a populated place we need to find the intersection of these two buffers¶

In [76]:
col_join = col_buffer.overlay(col_places_buffer)
col_join.head()
Out[76]:
featurecla scalerank LABELRANK_1 SOVEREIGNT SOV_A3_1 ADM0_DIF LEVEL TYPE TLC ADMIN ... FCLASS_ID_2 FCLASS_PL_2 FCLASS_GR_2 FCLASS_IT_2 FCLASS_NL_2 FCLASS_SE_2 FCLASS_BD_2 FCLASS_UA_2 FCLASS_TLC_2 geometry
0 Admin-0 country 0 2 Colombia COL 0 2 Sovereign country 1 Colombia ... None None None None None None None None None POLYGON ((-7881837.774 673851.953, -7893451.99...
1 Admin-0 country 0 2 Colombia COL 0 2 Sovereign country 1 Colombia ... None None None None None None None None None POLYGON ((-9195952.170 1390669.459, -9195635.0...
2 Admin-0 country 0 2 Colombia COL 0 2 Sovereign country 1 Colombia ... None None None None None None None None None MULTIPOLYGON (((-8467942.672 809172.032, -8468...
3 Admin-0 country 0 2 Colombia COL 0 2 Sovereign country 1 Colombia ... None None None None None None None None None POLYGON ((-7932201.846 668361.394, -7941592.04...
4 Admin-0 country 0 2 Colombia COL 0 2 Sovereign country 1 Colombia ... None None None None None None None None None POLYGON ((-8053621.414 681606.911, -8061656.19...

5 rows × 307 columns

In [77]:
col_join.plot()
Out[77]:
<Axes: >
No description has been provided for this image

With these polygons we can use spatial statistics and a raster of population to count the number of people. We will do this in GIS with Python 2.¶